November 2024 – April 2025
* Why Machines Learn: The Elegant Math Behind Modern AI, Anil Ananthaswamy, 2024. (Ananthaswamy is a science journalist, not an AI person, as I initially assumed. That said, he’s quite good.)
My Take on the Book
As discussed below, this is not the sort of book I’d usually read — my interest stops at the level or algorithms, and understanding the underlying math just doesn’t grab me. This really is a book for people interested in the math. But I learned some interesting, mostly-meta things from it.
- Early learning systems. Early research focused on using simple networks (e.g. Perceptrons) to recognize fuzzy inputs like hand-written letters. This involved presenting a system with an input, having it try to map that input to a category, and then providing feedback to the system based on the mismatch between the input and the right (label for the input) result. Much of the math to do with measuring and tracking the degree of error.
Even though they sound different things, this is also how adaptive filters: they try to learn the characteristics of noise so as to minimize it. - Matrices model networks! More generally, matrices and linear algebra are exceptionally useful for modeling networks.
- A Lot of AI learning is just gradient descent. A lot of the math involves figuring out multi-dimensional spaces that characterize a domain, and using some sort of algorithm, usually involving gradient descent, to find the minima. The minima, of course, being where error is minimized, meaning that the system is performing as well as possible at its learning task.
- People made jaw-droppingly crude simplifications, and yet the math still worked! Something I found very interesting was that, once you have an algorithm that appears to do what you want, you can make shockingly crude simplifications to it that (1) make it possible to run it in very high dimensional spaces, and (2) it will still work well.
For example, if you are doing gradient descent in a multi-dimensional space, you can get away with finding the gradient for a randomly chosen single dimension (stochastic gradient descent), rather than in all dimensions.
I still don’t get why that works, but it does. Not only does god play dice with the universe, but he’s OK with kludges tool. - Adding ‘noise’ can improve learning. Adding noise to data sets on which machines are trained can make the learning more robust. To me this seems sensible, in that, especially if you add different amounts of noise to the same features, you can multiply the training set and counter the tendency to overfit.
Of course the noise ought to be ‘natural,’ which is to say that it ought to be native to the distribution from which you are sampling. I presume it is possible to figure that out for particular domains, but don’t actually know. - Monty Hall as Enabling Inside Trading. Hurrah. I finally understand the Monty Hall problem. In my defense, I will note that the ‘story problems’ I had in my primary education worked against my ability to solve it. In story problems, the stories didn’t actually matter, they were just frameworks for presenting a math problem. But in the Monty Hall problem, the key bit is Monty — he has inside information and will not choose to spoil the game by revealing where the prize is. Thus his action is not random, and provides additional information. If the Monty Hall problem were instead re-presented as an earthquake or windstorm accidentally revealing a goat behind one of the doors, the answer would be different.
- WTF? — Why does deep learning work so well? We don’t, currently, really understand why deep learning works as well as it does. Spooky.,
- Why do deep neural nets keep learning new things after they’ve overfit their training data? In particular, there is the paradox of benign overfitting / harmless interpolation: a deep neural network has so many parameters that it should perfectly overfit the training data, but — after enough training — it is able to generalize correctly to new data, something that it would not do if it had overfit. So what is going on?
You’d think that once it was able to model the training data perfectly, it would stop learning. But perhaps the continued ‘training’ is introducing some kind of ‘noise’ or fluctuation which keeps perturbing the neural net? - Is something happening in the hidden layers??? I feel like there must be interesting stuff going on in the hidden layers of deep neural networks as their training continues beyond the point of benign overfitting/harmless interpolation. I don’t really understand what continued training of a deep neural net does — either directly or via back propagation. I have a vague idea idea that structure of the hidden layers undergoes some kind of phase change, in an analog to fractional crystallization. (In a magma chamber, where when the magma cools to a certain point a particular mineral crystalizes and precipitates, changing the nature of the magma and enabling further crystallization (and/or re-solution of prior crystalites) as the mix changes.)
- In the epilogue the author raises the questions of whether LLMs have really learned, or are just doing statistics. I’m in the “stochastic parrot” camp.
Context and Reflection
I am reading this book as part of a small book club: The 26-minute Book Club. This sort of book is really not my cup of tea — it is about the math with which various learning algorithms are implemented. I am, at my deepest, interested in the algorithms. Math is neither a strong point nor a deep interest — it seems more like magic to me: You generate a bunch of tautologies, define some terms and rules, and then elaborate it, and all of a sudden it enables you to do things.
I had imagined I would give this a one-meeting trial, and then bow out. However, I found the group (4 other people) quite pleasant, and composed of — barring the one person I know who invited me — interesting strangers that I would not otherwise get to know. And that, especially in retirement, is of great value.
Another advantage is that working through this book forces me to think about topics I would otherwise ignore: basic math including linear algebra, vectors, a little calculus, probability, gaussian distributions, Bayes’ Theorm. Perhaps it will prove tractable enough that I will feel emboldened to take on fluid dynamics, something that I suspect would help me better understand a whole range of natural patterns, from meteorological to geological…. Or perhaps I will figure out how to distill the ‘qualitative’ aspects that I am interested from the mangle of symbols. We shall see.
The Book
C1: Desperately Seeking Patterns
- Konrad Lorenz and duckling imprinting. Ducklings can imprint on two moving red objects, and will follow any two moving objects of the same color; or two moving objects of different colors, mutatis mutandis. How is it that an organism with a small brain and only a few seconds of exposure can learn something like this?
- This leads into a brief introduction to Frank Rosenblatt’s invention of Perceptrons in the late 1950’s. Perceptrons are one of the first ‘brain-inspired’ algorithms that can learn patterns by inspecting labeled data.
- Then there is a foray into notation: linear equations (relationships) with weights (aka coefficients) and symbols (variables). Also sigma notation.
- McCulloch and Pitt, 1943, story of their meeting, and their model of a neuron — the neurode — that can implement basic logical operations.
- The MCP Neurode. Basically, the neurode takes inputs, combines them according to a function, and outputs a 1 if they are over a threshold theta, and a 0 otherwise. If you allow inputs to be negative and lead to inhibition, as well as allow neuroses [sometimes spell-correct is pretty funny] to connect to one another, you can implement all of boolean logic. The problem, however, is that the thresholds theta must be hand-crafted.
- Rosenblatt’s Perceptron made a splash because it could learn its weights and theta from the data. An early application was to train perceptrons to recognize hand drawn letters — and it could learn simply by ‘punishing’ it for mistakes.
- Hebbian Learning: Neurons that fire together, wire together. Or, learning takes place by the formation of connections between firing neurons, and the loss or severing of connections between neurons that are not in sync.
- The difference between the MCP Neurode and Perceptrons is that perceptrons input’s don’t have to be 1 or 0 — they can be continuous. And they are weighted, and they are compared to a bias.
- The Perceptron does make one basic assumption: that there is a clear, unambiguous rule to learn — no noise in the data. If this is the case, it can be proven that a perceptron will always find a linear divide (i.e. when there is one to be found).
C2: We are All Just Numbers
- Hamilton’s discovery of quaternions, and his inscription on Brougham bridge in Dublin. i2 = j2 = k2 = ijk = -1 Quaternions don’t concern us, but Hamilton developed concepts for manipulating them that are quite important: vectors and scalars.
- Scalar/Vector math: computing length; summing vectors; stretching a vector by scalar multiplication;
- Dot product: a.b = a1b1 + a2b2 (the sum of the products of the vector’s components). The dot product (AKA the scalar product) is an operation that takes two vectors and returns a single number (a scalar). It’s a way to quantify how much two vectors “align” with each other — that is, the degree to which they point in the same direction.
- E.g. Imagine pushing a model railroad car along some tracks. If you push in the exact direction that the tracks go, all the force you apply goes into moving the car; if you push at an angle to the tracks, only a portion of the force you apply goes into moving the car. This (the proportion of force moving the car along the tracks), is what the dot product gives you.
- Something about dot products being similar to weighted sums, which can be used to represent perceptrons??? Didn’t understand this bit. [p. 36-42]
- A perceptron is essentially an algorithm for finding a line/plane/hyperplane that accurately divides values into appropriately labeled regions.
- Using matrices to represent vectors. Matrix math. Multiplying matrix A with the Transpose of Matrix B
- So the point of all this is to take Rosenblatt’s Perceptron and transform it into formal notation that linearly transforms an input to an output.
- “Lower bounds tell us about whether something is impossible.” — Manuel Sabin
- Minsky and Papert’s book, Perceptrons, poured cold water on the field by proving that Perceptrons could not cope with XOR. XOR could only be solved with multiple layers of Perceptrons, but nobody knew how to train anything but the top layer
- I am not clear on why failure to cope with XOR was such cold water…
➔ Later: It is because XOR is a simple logical operation; the inability of Perceptrons handling it suggested that they would not work for even moderately complex problems. Some also generalized the failure to all neural networks, rather than just single layer ones. - Multiple layers requires back-propagation…
C3: The Bottom of the Bowl
- McCarthy, Minsky, Shannon and Rochester organized the 1955 Dartmouth summer seminar on Artificial Intelligence. Widrow attended this seminar, but decide it would take at least 25 years to build a thinking machine,
- Widrow worked on filtering noise out of signals: He worked on adaptive filtering, meaning a filter that could learn from its errors. Widrow worked on continuous signals; others applied his approach to filtering digital signals. Widrow and Hoff — Adaptive filtering — invented Least Mean Squares algorithm.
- Least Mean Squares is a method for quantifying error. What Widrow wanted to do was to create an adaptive filter that would learn in response to errors — this required a method for adjusting parameters of the filter so as to minimize errors. This is referred to as The Method of Steepest Descent, discovered by the French mathematician, Cauchy.
- Much of the rest of the chapter introduces math for ‘descending slopes.’ dx/dy moves us along a gradient… the minimum will have a slope of zero. When we have planes or hyperplanes we need to take multiple variables into account so we have partial derivatives.
“If there’s one thing to take away from this discussion, it’s this: For a multi-dimensional or high-dimensional function (meaning, a function of many variables), the gradient is given by a vector. The components of the vector are partial derivatives of that function with respect to each of the variables.
…
What we have just seen is extraordinarily powerful. If we know how to take the partial derivative of a function with respect to each of its variables, no matter how many variables or how complex the function, we can always express the gradient as a row vector or column vector.Our analysis has also connected the dots between two important concepts: functions on the one hand and vectors on the other. Keep this in mind. These seemingly disparate fields of mathematics-vectors, matrices, linear algebra, calculus, probability and statistics, and optimization theory (we have yet to touch upon the latter two) – will all come together as we make sense of why machines learn.”
…Reading Break…
- So with an adaptive filter, you filter the input, and look at the error in the output, and feed that error back into the filter, which adjusts itself to minimize the error.
- So first you need to be able to have an input where you already know what the true signal is, so that you can determine the error after the filter has transformed the input. How do you get that? ➔ Later: In the application we’re talking about, this is the training phase. Once the model is trained, you assume the characteristics of the noise will not change and the model will continue to work.
One issue is whether the noise in the signal is always of the same sort — that is, if you train an adaptive filter on a bunch of inputs whose signals you know, will that give you a good chance of having a filter that can appropriately transform an unknown signal? The book uses the example of two modems communicating over a noisy line, and it makes sense (I think) that noise would have fairly uniform characteristics, at least for the session. But that seems unlikely to hold for everything. Can we assume that the noise, in a particular situation, is always the same ,or at least has the same statistical properties?
Suppose the source or nature of the noise in the signal changes over time? Well, you could embed some kind of known signal into the input (I imagine, say, a musical chord), and let the filter learn to adjust the output so that the known chord comes through. But will a filter that preserves the chord also preserve the other information in the signal? I have no idea. I’d think it would depend a lot on (1) the nature of the signal, and (2) the nature of the noise. - I’m confused about the part about adding delays to signal… and I’m confused about how, in real life, you know what the desired signal is.
- ➔ Later: Still not very clear on the noise issue, but I’m guessing it depends on what you’re applying it to. If the noise is varies in an unpredictable way for a particular application, then the filter/neuron simply won’t work and will produce gibberish.
- Anyway, let’s assume we know the desired signal (and hence the noise/error) — how do we quantify the later? We don’t want to just add it up because it can have positive or negative values which would cancel one another out — instead, the errors are squared, and you take their mean to quantify the noise: the is called the Mean Square Error. It is also the case that squaring the errors exaggerates the effects of the larger errors, which seems like a desirable thing.
- The math shows that the formula for the error associated with an adaptive filter is quadratic, meaning that it will be concave, and that thus the minimum error will be the minimum of the function. That can be found in multiple ways, either by finding the point at which the slope of the function is zero, or using gradient descent to find it.
- A problem is that to do this, you need more and more samples of xn and yn and dn to calculate parameters, and you need to use calculus to calculate partial derivatives, and especially in high dimensional space this becomes burdensome (or impossible).
- The solution was that Widrow and Hoff found a (IMO kludgy) way to just estimate the error without doing a lot of work.
weightNew = weightOld + 2 • <step-size> • <error-for-a-single-point>
- This is called the Least Mean Squares (LSM) algorithm.
➔ Later: What they are doing is taking a single data point(a single input-out put pair) at random and using that to estimate the gradient and adjust the weight. Each update a new pair is randomly selected, and over time the algorithm noisily decreases the error. This is called Stochastic Gradient Descent. There is an alternative to this approach called mini-batch gradient descent that uses a randomly-selected set of points (e.g. 32 of them) for each update.
C4: In All Probability
- The Monty Hall problem. There are three doors, one of which has a valuable prize behind it, and the others which have only goats. After you’ve picked door 1, Monty opens door 2, revealing a goat. You now have a change to change your pick — should you do that?
- The answer. The answer is “yes.” For a long time this seemed counterintuitive to me (and Paul Erdos): revealing what is behind one of the doors should not change the probability of what is behind the other doors. What was tripping me up (ironically) is that I was ignoring the psychology. The key is that Monty is not opening a door at random: he knows what is behind each door, and in particular, he will not open a door that has the prize behind it (as that would destroy the game). So when Monty opens door 2, he is sometimes providing information about both door 2 and about door 3.
- Let’s suppose I’ve picked the first door. There are three cases:
(1) Pxx — if I have the correct door, Monty can open either of the others.
(2) xPx — If a goat is behind 1, and P behind 2, Monty can only open 3
(3) xxP — If a goat is behind 1, and P is behind 3, Monty can only open 2
In 2 of these 3 cases, switching to the remaining unopened door gets me the prize. Monty has change the prior probabilities, and so we much re-evaluate. - This argument will hold for any number of doors, because Monty always knows where the car is, and since he will avoid opening that door, every door he opens changes the priors — i.e. gives additional information about the unopened doors.
- Later: If we construct a different version of the problem, where, before Monty can pick a new door, an earthquake strikes and door 2 happens to collapse, revealing the goat, there is no reason to change (or not change) your pick. The revelation of the goat behind door 2 does not give us further information about what is behind any of the other doors, since the earthquake’s ‘revelation’ was truely a random event.
- Bayes Theorem history. Interestingly, Thomas Bayes’ essay describing his approach was only presented to the Royal Society in 1763, two years after his death, by his friend Richard Price (who later scholars believe made substantive contributions, although Price attributed it all to Bayes).
P (X-is-true | given Evidence-for-X is positive)
IS EQUAL TO
P-X-in-the-world • How-strong-the-evidence-is (e.g. the accuracy of the test)
————————————- (DIVIDED BY) —————————————————-
(P-X-in-the-world • probability of a true positive)
• (1 – P-X-in-the-world) • (1 – probability of a true positive)
OR
The empirical probability in the world * the predictive accuracy given evidence
————————————————————————————————————————–
the likelihood of the world producing that evidence
(=sum of probabilities of all ways of producing that evidence)
…Reading Break…
- Machine Learning is inherently probabilistic because there are an infinite number of hyperplanes that can discriminate between a learned alternative, and it has settled on one of them for no particular reason. Other factors that make ML less than accurate are that the data itself may have errors, and that the amount of data drawn upon is limited. Later: And we must keep in mind that ML is only minimizing error — whether the result has enough signal to be useful is an empirical and domain-dependent issue.
- Distinction between theoretical probability and empirical probability (e.g., theoretical probability of a fair coin coming up heads is 50%; empirical probability of a fair coin coming up heads depends on actually doing it, and it will approach but not reach the theoretical probability as one increases the number of empirical samples.
- Aside: There is also the issue of the degree to which real-world events are actually expressions of mathematical distributions. It seems elegant to assume that, but is it really so?
- The case of a coin flip is an example of a Bernoulli distribution. It has only two values, a and b, and can be characterized by a probability p that such that p is the probability of a, and (1–p) is the probability of b.
- Distributions with a mean and a variance (aka standard deviation). Now consider the case where you have N>2 outcomes, each with their own probability. This is distribution can be characterized by a mean and standard deviation — the mean (aka the expected value) is the sum of the values of each outcome multiplied by their probabilities, and the standard deviation is the square root of {the sum of the squares of the (deviations of each value from the mean)} — or the sum of the absolute value of each values difference from the mean. We can talk about the distribution as a whole in terms of its probability mass function.
- So far we’ve been talking about variables with discrete values, but we can instead talk about variables with continuous values. Here we can’t talk about the probability of a particular value because there are an infinite number of values and the probability of any single perfectly precise value is zero. So, instead, what we do is talk about the probability of a value occurring within particular bounds: this is called the probability density function. [Aside: But wouldn’t it be possible to do some calculus like move where we look at what happens as a finite interval approaches zero?]
- The important point is that whether we have a variable with discrete or continuous values, we can use well-known and analytically well understood functions to characterize the distribution.
- Machine Learning. Let’s being with a set of labeled data points: y is a label that has two values, and x is an instance of the data. y is categorical; x is a vector with N components. This data set can be represented as a matrix: y1, x11, x12, x13 .. x1n and so on for y2, y3, etc. Each component of x is a feature that the algorithm will use to discriminate which y x belongs to.
- Now, if you knew the underlying distribution P(y, x), you could determine the probability of y=A given x, and the probability of y≠A given x, and use the highest probability to assign the label. If this were the case, this is what would be termed a Bayes Optimal Classifier. [Aside: I’m a little unclear on this — it seems like it’s dependent on a particular situation, and so it seems odd to give it this sort of name.]
- But usually you don’t know the underlying distribution, and so it must be estimated. Often it is easier to make assumptions about the underlying distribution (Bernoulli? Gaussian?), but it is important to keep in mind that these are idealizations chosen to make the math easier.
- Aside: A Gaussian distribution is defined as being symmetric with respect to a single mode (which is also the mean and median), with asymptotic tails that never reach 0.
- There are two approaches to estimating distributions:
One is MLE or Maximum Likelihood Estimation, involves selecting a theta (that is a distribution with particular parameters indicated by theta) that maximizes the likelihood of observing (generating?) that labeled data you already have.
In the text, MLE is exemplified by imagining a set of data about two populations’ heights, labeled short or tall, and that each population has a gaussian distribution, and thus that all the data will be best modeled by a combination of the two distributions. ???But is that still a gaussian distribution? And what is the rational for choosing a gaussian distribution rather than some other distribution???
The other is called MAP, for Maximum A Posteriori estimation. As best I can tell, this involves estimating the distribution based on our experience of the world and representing it as a function. Then you set the derivative to zero, and solve that equation (after checking to be sure that you’ve got the maximum rather than the minimum). If this approach does not yield a ‘closed’ solution (most of the time), you can take the negative of the function and use gradient descent to find its minimum. - MLE vs MAP. So MLE tries to find the maximum using the data, and MAP tries to find the maximum of a distribution you’ve guessed at. MLE works best when there’s a lot of data; MAP works best when there isn’t much data you can make a reasonable guess about the underlying distribution).
- The Federalist Papers example: which unattributed papers were written by Madison and which by Hamilton. A first approach was to analyze the length of sentences in papers know to be written by each author, and use the mean length and the standard deviation to discriminate: unfortunately the means and SDs for each author were almost identical. Later, someone suggested using the frequency of word use, and, in particular, function words tended to reliably discriminate between the known works of the two authors: this was then used to predict which of the unattributed essays were written by which author.
- Aside: It is not clear to me whether the achievement of Mosteller and Wallace was due to the use of Bayesian reasoning, or to the realization the word choice was a very good discriminator between the authors. ➔ LATER: Consensus among scholar from many fields indicates, according to chatGPT, that their work did indeed validate the use of Bayesian inference, as well as creating a new approach to linguistics, and indicating the ways in which computers could be used.
- The Penguin example.
- A trick that statisticians use is to assume that the distributions for each feature under consideration are independent — seems like a bit of a leap, but it appears to work and it makes the math easier and requires less data.
- Naive or Idiot Bayesian classifier.
… reading break…
C5: Birds of a Feather
- The 1854 Snow Cholera Epidemic map
- Voroni diagrams and nearest neighbors
- When you represent something as a set of N-dimension vectors, the vectors can be considered as points in an n-dimensional space, and you can use the NN algorithm to compute their neighbors, and devise non-linear boundaries between labeled points.
- However, as the dimensionality of the space increases, there’s a problem in that the space, in most regions, becomes very sparsely populated…
… reading break…
C6: There’s Magic in Them Matrices
- Principal components analysis (PCA) involves reducing the dimensionality of a data of space in such a way that the retained dimensions capture most of the variance.
- This assumes that dimensions that do not contain much variance are unimportant; and that the dimensions that capture a lot of variance actually are important. This may not be true.
- A few notes on Vectors
- A vector with six components as a dimensionality of six. That is, it can be represented by a single point in a six dimensional space.)
- Multiplying a vector by a square matrix of the same dimensionality, basically means changing the magnitude and orientation of that vector in the same space.
- An eigenvector of a matrix is a non-zero vector such that, when it is multiplied by the matrix, it does NOT change its orientation, only its length. The length of the eigenvector is called the eigenvalue.
- Basically, for any matrix of dimension N, you can find N eigenvectors that, when multiplied by the matrix, do not change orentation, but only change magnitude (that magnitude is the eigenvalue)
- For a symmetric matrix, the eigenvectors lie along the major and minor axes (hyperaxes) of the (hyper)ellipse.
- There is a nice visualization on pages 186-187 of what it means to find the eigenvectors
- Centering a matrix means taking the mean for a particular dimension (feature) and subtracting that from each individual value for that feature: that transforms each feature’s value into how much it deviates from the mean. This is also called “mean corrected” matrix.
- If you multiply a mean, corrected matrix by its transpose, you get a square matrix where the diagonal values showed the variance for each feature, and the off diagonal values show the covariant between pairs of features. This is called the mean-corrected ovarian matrix.
- Now, if you compute the eigenvectors for that matrix, the eigenvalues will allow you to see where most of the variance is and do a principal components analysis, reducing the dimensionality of the matrix.
… reading break…
Actually, a break of about six weeks
during which I was traveling and missed the group meetings.
I may go back and summarize the missed material… or I may not not.
C7: The Great Kernel Rope Trick
The first part of the chapter talks about developing an algorithm for finding the optimal hyperplane that separates two groups. The improves on what a perceptron does — it finds a hyperplane, but not necessarily (and probably not) the optimal one. The algorithm here works by maximizing the margin or border between the closest points.
The kernel trick refers to computing the dot products of vectors in higher dimensional spaces by computing the dot products of lower-dimension vectors that are mappings from the original vectors. This is significant because one way of classifying sets of data that overlap is by projecting them into higher dimensional spaces where they don’t overlap, and figuring out the optimal hyperplane there — except the kernel trick allows you to calculate the hyperplane without doing in the high-dimensional space. The term used for this technique is Support Vector Machines.
C8: With a Little Help from Physics
Hopfield Networks. Networks that have local energy minima that represent ‘memories.’ When a new input comes that produces something close to a particular memory, that pattern is likely to ‘decay’ into the stable pattern that represents the memory.
Hopfield’s work showed that the brain could be modeled as a dynamic system.
C9: The Man Who Set Back Deep Learning (Not Really) – TBD
C10: The Algorithm that Put Paid to a Persistent Myth – TBD
C11: The Eyes of a Machine
- Hubel and Weisel’s work on the visual cortex of cats beginning with the serendipitous discovery of edge detection. They described a neural architecture in which a hierarchy of cells detected increasingly complex visual features based on multiple simple detectors feeding into more complex detectors.
- This architecture was used in neural nets…
- The convolution operation enabled the mathematical mimicking of detectors using the convolution matrices (aka filters).
- Cu Lin figured out how to create networks that could learn their own filters…
C12: Terra Incognita – TBD
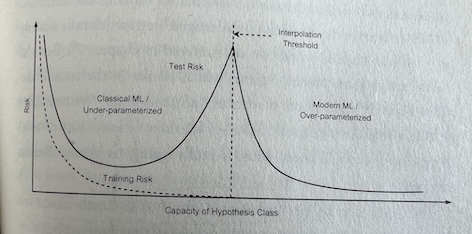
- Overfitting — a rule that essentially involves learning every single piece of data that the algorithm was trained on. Models that have overfit (or approach overfitting) their training data are said to have high variance; models that underfit the data are said to have high bias.
- Grokking. It appears that when you ‘overtrain’ neural networks, they go beyond overfitting and instead generalize in different ways. The example in the chapter has to do with someone going on vacation and leaving a training algorithm running, and discovering that it had discovered a more general solution for the data set it was being trained on (mod 93 addition). This is called grokking, a term I hate.
- “If an algorithm’s task is to identify a chair, it should not matter what they are made of.” Not necessarily…
- Deep neural networks have way too many parameters — they ought to overfit their data, and should not generalize well. But, in fact, they do generalize well. We don’t really understand why. Oddly, even if you add more parameters than there are instances of training data, generalization does not get worse.
- Benign overfitting. If you intentionally introduce noise into the training dataset, and train the model so that it fits the training data perfectly, the model is said to “shatter” the training data because it has learned both the data and the noise. Yet such models can have as much as 5% noise in their training datasets and still work well on new data.
- It seems to me that introducing noise ought to promote generalization. Claude.io: “Research has confirmed that “the addition of noise to the input data of a neural network during training can, in some circumstances, lead to significant improvements in generalization performance.” This works as a form of regularization that improves the model’s robustness.” But it depends on the proportion of noise (too much and too little are both problems), and things work better if the noise is only in the features and not in the labels.
- Parameters (in the model) vs. Hyperparameters (chosen before hand — like the architecture and numbers of layers and nodes in the network).
- Self-supervised learning — where the network figures out labels for the data from the data. E.g. Chat GPT takes a sentence, masks out a single word, and then tries to learn the missing word.
- The Paradox of Benign Overfitting / Harmless Interpolation
Epilogue
Reflection on LLMs and what they’re doing — are they learning or just doing statistics? I’m in the “stochastic parrot” camp. Also comments on problems with LLMs, e.g., they mirror prejudices baked into the training data. I find some of the statements here — to wit “its clear the LLMs are beginning to show some hints of a theory of mind” dubious.
Also a brief bit on using neural networks to model the neural architecture of monkeys and their responses to various classes of visual stimuli — there has been some success (including at constructing artificial stimuli) that perform similarly in both computation models and brains…
Views: 16
